Transformers identifying kernel structures
A review paper on find kernel structure using deep neural network
In this post, I will review a recent paper
Kernel structure discovery has been one of my main research topics
In learning Gaussian process, selecting kernels (kernel types or kernel structure) is important because the kernel types may encode inductive bias, i.e., periodicity, trends in data. Previous work often requires extensive search procedure to select an appropriate kernel. The proposed approach in this paper
One-sentence description DNNs inspired by transformer architecture satisfying permutation invariance are trained over samples generated from kernel priors, minicking image-caption task to predict kernel structure.
Kernel structures in Gaussian Process
When talking about kernel structures, we mean what types of kernel function are. Kernel functions are constructed from base kernels into compositional kernels.
Base (primitive) kernels are showed in this kernel
| Kernel name | Kernel function |
|---|---|
| Squared exponential | \(\sigma^2 \exp(-(x-x')^2/2\ell^2)\) |
| Linear | \(\sigma^2 (x - \ell) (x' - \ell)\) |
| Periodic | \(\sigma^2 \exp (\sin^2((x-x')/p)/\ell^2)\) |
The compositional kernels are obtained by using addition or multiplication over base kernels because the closure property of kernel methods. The space of such kernel functions is open-ended.
The more complex kernel structures is, the more expressive the corresponding Gaussian process model cound become.
Note that each base kernel encodes their own intrinsic characteristics which can be translated into nouns. Therefore, compositional kernels can be noun phrases.
Prepare data
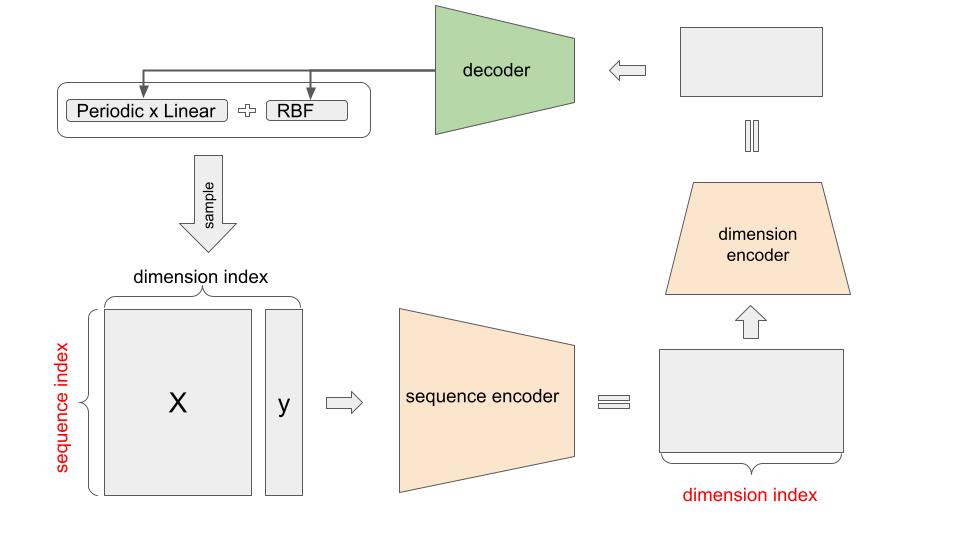
Starting off with building a set of kernel functions which is “reasonably large” enough, we sample priors to produce data $X, y$. This pair is concatenated side by side, and visually looks like an image.
\[\text{Image} \to \text{Caption} \qquad \Rightarrow \qquad \text{Sample} \to \text{Kernel Structure}\]The kernel structures here are the name of additive kernels composed from a set of vocabulary of kernel names.
Model architecture
Permutation Invarance
The sum running over index $i$ enables the invarance when we permute $x_i$. In practice, we often encounter problems that the orders of elements in sets does not matter. If a model considers ordering dependency, it’s bound to subjectively fail. This concept is closely related to de Finetti’s theorem on exchangeability of random variables. Here $\rho, \phi$ are parameterized with neural networks.
Double permutation invariance (over data index and dimension index) The paper aims to have invariance over not only data (sequence) indices but also dimension indices.
\[f(\mathbf{X}) = \rho\left( \sum_i \rho' \left(\sum_j \phi'(X_{ij})\right) \right)\]Encoder
Encoder consists of sequence encoder and dimension encoder. These two serve the above double permutation invariance
- Sequence Encoder is built upon attention mechanism (like previous post ) and a mean pooling.
This uses the set transformer approach from
- Dimension Encoder is responsible for the permutation invariance over dimension indices
Formally, encoder is constructed as
\[Encoder(X) = g(f(X)).\]Decoder
Decoder has the responsibility to reproduce kernel structures as sentences out of the predefined set of “kernel” vocabularies. The model architecture of decoders is similar to “Attention is All You Need” paper
Conclusion
If the proposed method really works well in practice, we no longer have to wait hours to search over kernel structure space, but just train a neural network helping us to obtain most probable candidates quickly (in seconds).
Despite of being able to generate kernel structure on the fly, it’s hard to conclude that the obtained kernel structures agrees with the tradition principles in model selection prefering simple models over complex ones like Bayesian Information Criteria, or Occam’s razor.
Athough experiment section contains extensive results. I feel that the demonstration for the most simple case where we only consider time series should be presented. Probably, to work on 1D data set, the architectures of transformers do not have to satisfy double permutation invarance.
Although the permutation invariance over dimensions is nice, the concatenation of $X$ and $y$ may ignore the dependency between $X$ and $y$. For example, the model may not know the causual relationship between $X$ and $y$.